组织属于心血管系统表现出粘弹性行为,由于叠加的弹性和粘性的组件,因此,机械能的传播在整个系统分为两个部分:一个可以存储在组织和检索由于弹性,而第二部分是由于粘性耗散。
本文旨在介绍分数展示在心血管系统粘弹性的分析中的分数微积分提供的可能性。
动脉显示粘弹性行为,使得由于动脉壁的弹性和粘性部件而透射的能量均储存和耗散[1-7]。该行为的知识和弹性和粘性组分的知识可能对影响心血管系统的退行性疾病的物理病理机制至关重要。
关于这一主题发表的第一个相关研究研究了狗动脉的静态和动态粘弹性行为[1,2]发表了一项里程碑式的研究,通过分析不同频率下半径和压力之间的相关性来检查狗动脉的粘弹性。他观察到基于脉搏波频率的动态弹性模量(杨氏)和动脉壁的肌肉成分显著增加。特别地,由于杨氏模量为[3]:

在哪里 是由压力变化引起的外部半径的变化
是由压力变化引起的外部半径的变化 是内部半径,是泊松比,例如泊松比。横向于轴向菌株的比率。杨氏的等式(1)模量可以分别分成弹性和粘性组分[2]EC和ES.,由
是内部半径,是泊松比,例如泊松比。横向于轴向菌株的比率。杨氏的等式(1)模量可以分别分成弹性和粘性组分[2]EC和ES.,由

α是压力变化与外部半径膨胀之间的相,η是粘度之间的相,ω是脉动之间的相,例如2π乘以频率。ν
使用涉及弹簧(代表弹性)和DASHPOTS(代表粘度)的数学建模和平行的数学建模进行动脉的力学行为的模拟。在弹簧中,应力σ和应变ε之间的关系由等式给出

而在阻尼器中,关系是

象征 表示时间衍生物。弹簧和划线波的主要组合是Maxwell模型(Spring in系列)和voigt模型(一个平行的弹簧和小截面)[5]。
表示时间衍生物。弹簧和划线波的主要组合是Maxwell模型(Spring in系列)和voigt模型(一个平行的弹簧和小截面)[5]。
麦克斯韦模型,有春天年代和阻尼器D串联的特点是总应力等于两个元素中的应力,这必须是相同的,这样 ,而总菌株由单个菌株的总和给出,得到
,而总菌株由单个菌株的总和给出,得到 ,应变的时间变化是
,应变的时间变化是

当然是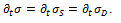
相反,在Voigt模型中,总应力由单个应力的总和给出,例如: 总应变是
总应变是 所以重音可以写成这样的形式:
所以重音可以写成这样的形式:

进一步的模型,称为标准线性固体(SLS)模型[6],结合了麦克斯韦模型和一个平行的弹簧。如果平行弹簧的杨氏模量是EP.,麦克斯韦州模型中的弹簧的模量是E米,那么管理标准线性实体模型的等式

分数阶微积分是数学分析的一个分支,研究给定函数的分数阶导数和积分。在第一近似值中,当两种或两种以上的物理效应相互叠加,因此两者都要考虑时,可以使用它。
一个简单的解释分数阶微积分[8]是如何产生的方法可以通过知道一个函数的n阶导数而得到

在哪里 是欧拉伽玛功能,m!表示M,例如产品M(m -1)... 1的阶乘。我们可以推断
是欧拉伽玛功能,m!表示M,例如产品M(m -1)... 1的阶乘。我们可以推断

实际上,函数是阶乘的一般化,并根据复变量z的定义定义其任何可能的值

从这些处所开始,瑞士数学家Leonhard Euler,1730年指出,等式(3)中的定义允许计算分数顺序的衍生物。使用该价值 欧拉获得
欧拉获得

使用相同的欧拉的程序,然后可以计算任何顺序的衍生物,例如衍生物yπ订单E.,如下所示

更一般地,我们可以用一个函数的α阶分数阶导数的定义 由于Riemann-Liouville As
由于Riemann-Liouville As

相同的推理可能导致非整数顺序的积分定义,因为 - 基于RIEMANN-LIOUVILLE定义第n个订单集成 - 我们可以为整数N和可集成功能编写 :
:

将积分推广到分数阶φ,得到:

这使我们能够整合 非整数次数[8-10]。
非整数次数[8-10]。
分数微积分对动脉粘弹性研究的应用
用分数阶微积分分析物体的粘弹性行为,从定义应变的分数阶导数的可能性开始,从分数阶导数可以得到等效形式的应力:

在哪里 是时间不变,而在
是时间不变,而在 具有这些特性的元素被定义为弹簧壶[11],因为它同时具有弹簧和阻尼器的特性。
具有这些特性的元素被定义为弹簧壶[11],因为它同时具有弹簧和阻尼器的特性。
Craiem和合作者[12]对式(2)作拉普拉斯变换,采用复杨氏模量 在频域,由
在频域,由

从等式(2)开始,分数微分方程在形式中统治弹簧盆

其中应力-应变关系为

而复杂杨氏模量的分数形式是

使用该数学框架,其中弹簧盆取代了标准线性固体模型的笨蛋,然后可以使用来自捐助者的人升性的人类升序的一些段来验证实验结果,不用于动脉粥样硬化相关的原因[11],获得价值 在两个不同的实验水平的压力。
在两个不同的实验水平的压力。
诸多模拟的可能性在对健康以及人体血管的病理行为的研究中可能有用:弹性模量对各种组织和器官的血液传输产生显着影响。因此,人们希望在研究中,分数微积分将是至关重要的,例如,当任何原因,壁的弹性部件沿动脉突然变化时:例如,如此,例如,肾移植后肾动脉的连接[13],或者由于生理或病理因素增加应力[14-16]。
- BERGEL DH(1961)动脉壁的静态弹性性质。j physiol.156:445-457。[crossref]
- BERGEL DH(1961)动脉壁的动态弹性特性。j physiol.156: 458 - 69。[crossref]
- 《弹性数学理论的论述》,第4版,纽约,多佛出版社。
- Rubenstein da,Yin W,框架MW(2012)生物流体力学。学术出版社,牛津。
- 王志强(2016)心血管组织的粘弹性特性,中华医学杂志。InTech,里耶卡。
- 生物力学对骨科临床实践的贡献。Conf Proc Ieee Eng Med Biol Soc7: 5455。[crossref]
- Fung YC(1997)生物力学:流通,第二次。春家韦尔格,纽约。
- Oldham KB,谱扳手J(1997)分数微积分。学术出版社,纽约。
- Podlubny i(1999)分数微分方程。学术出版社,圣地亚哥。
- Mainardi F(2010)线性粘弹性的分数微积分和波浪。伦敦帝国学院出版社。
- Koeller RC(1984)分数微积分对粘弹性理论的应用。J:机械工程51: 299 - 307。
- Craiem DO, Rojo FJ, Atienza JM, Guinea GV, Armentano RL(2008)分数阶微积分在动脉粘弹性模型中的应用。拉丁美洲苹果申请38:141-145。
- Pallotti G,Donati G,Capelli I,Baraldi O,Comai G,等。(2015)供体/受体三角洲年龄:肾移植中动脉狭窄的可能风险。计算数学方法Med2015:512929。
- 肖华,谭毅,李东,等。(2017)导管动脉脉搏波速对心率依赖性的影响。Am J Physiol Heart Circ Physiol312: h1185 - 1185 h1194。[crossref]
- (2016)基于各向异性多凸超弹性和各向异性粘弹性模型的动脉流固耦合数值模拟。INT J数方法生物密32。
- Taniguchi R,Hosaka A,Miyahara T,Hoshina K,Okamoto H,等。(2015)颈动脉血管壁的粘弹性劣化是冠状动脉疾病的可能预测因子。J Atheroscler Thromb22:415-423。[crossref]



 是由压力变化引起的外部半径的变化
是由压力变化引起的外部半径的变化 是内部半径,是泊松比,例如泊松比。横向于轴向菌株的比率。杨氏的等式(1)模量可以分别分成弹性和粘性组分[2]EC和ES.,由
是内部半径,是泊松比,例如泊松比。横向于轴向菌株的比率。杨氏的等式(1)模量可以分别分成弹性和粘性组分[2]EC和ES.,由


 表示时间衍生物。弹簧和划线波的主要组合是Maxwell模型(Spring in系列)和voigt模型(一个平行的弹簧和小截面)[5]。
表示时间衍生物。弹簧和划线波的主要组合是Maxwell模型(Spring in系列)和voigt模型(一个平行的弹簧和小截面)[5]。 ,而总菌株由单个菌株的总和给出,得到
,而总菌株由单个菌株的总和给出,得到 ,应变的时间变化是
,应变的时间变化是
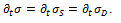



 是欧拉伽玛功能,m!表示M,例如产品M(m -1)... 1的阶乘。我们可以推断
是欧拉伽玛功能,m!表示M,例如产品M(m -1)... 1的阶乘。我们可以推断

 欧拉获得
欧拉获得

 由于Riemann-Liouville As
由于Riemann-Liouville As



 是时间不变,而在
是时间不变,而在 具有这些特性的元素被定义为弹簧壶[11],因为它同时具有弹簧和阻尼器的特性。
具有这些特性的元素被定义为弹簧壶[11],因为它同时具有弹簧和阻尼器的特性。 在频域,由
在频域,由



 在两个不同的实验水平的压力。
在两个不同的实验水平的压力。